INTRODUCTION
Combinatorial logic circuits are digital circuits that perform logical operations on a set of inputs to produce a set of outputs. These circuits are called combinatorial because their outputs depend only on the current state of the inputs, and not on any previous inputs or outputs. Two of the most basic combinatorial logic circuits are the half adder and the full adder.
HALF ADDER :
A half adder is a combinatorial circuit that performs the operation of addition of two single binary digits (bits). It has two inputs, A and B, and two outputs, S (sum) and C (carry). The truth table for a half adder is as follows:
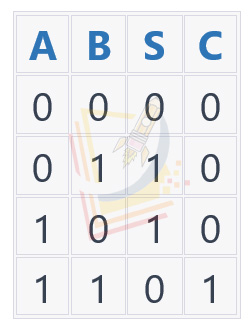
As we can see from the truth table, the output S is the XOR of inputs A and B. The output C is the AND of inputs A and B.
FULL ADDER:
A full adder is a combinatorial circuit that performs the operation of addition of two single binary digits (bits) and also take into account a carry input. It has three inputs, A, B, and Cin (carry in), and two outputs, S (sum) and Cout (carry out). The truth table for a full adder is as follows:
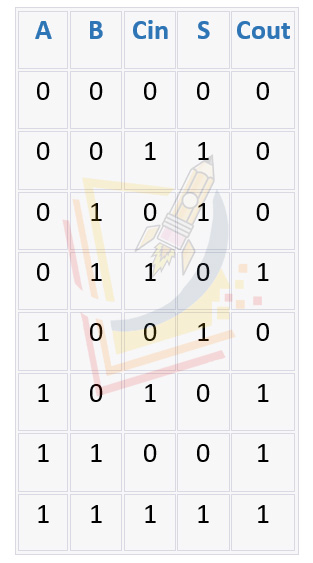
As we can see from the truth table, the output S is the XOR of inputs A, B and Cin. The output Cout is the OR of (A AND B), (Cin AND (A XOR B))
CONCLUSION :
In conclusion, the half adder and full adder are two basic combinatorial logic circuits that perform the operation of binary addition. The half adder adds two single binary digits and produces a sum and a carry output, while the full adder adds two single binary digits and also takes into account a carry input, producing a sum and a carry output. These circuits form the building blocks for more complex digital systems such as binary counters, adders, and subtractors.
